E | ngineering
자료구조/알고리즘
덞웖이
2024. 10. 1. 16:39
*코드블럭 한 항목씩 없애는 중임... (지재권)
Algorithms
Binary Search
더보기
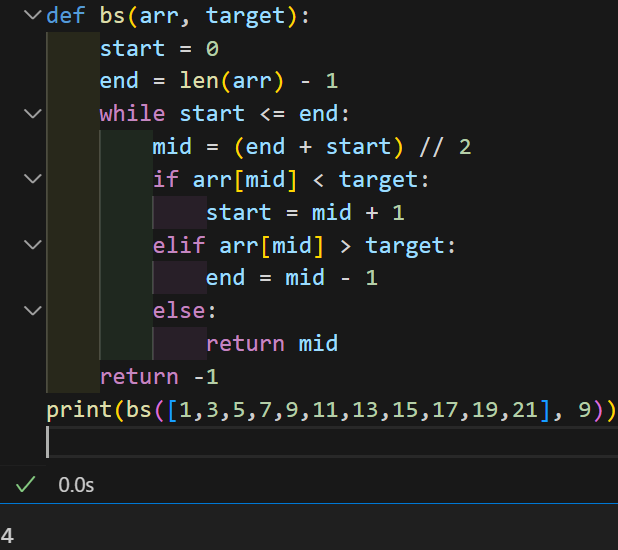
다른 문제로 풀어봄.
반씩 쪼개면서...
edit: 원본의 idx = -1 삭제, 필요없는 조건문 삭제

Fibonacci Sequence
더보기
def solution(x):
if x == 0 or x == 1:
return x
else:
return solution(x - 1) + solution(x - 2)Recursive Binary Search
더보기
def solution(L, x, l, u):
if l > u:
return -1
mid = (l + u) // 2
if x == L[mid]:
return mid
elif x < L[mid]:
return solution(L, x, l, mid - 1)
else:
return solution(L, x, mid + 1, u)Infix to Postfix Conversion Using Stack
더보기
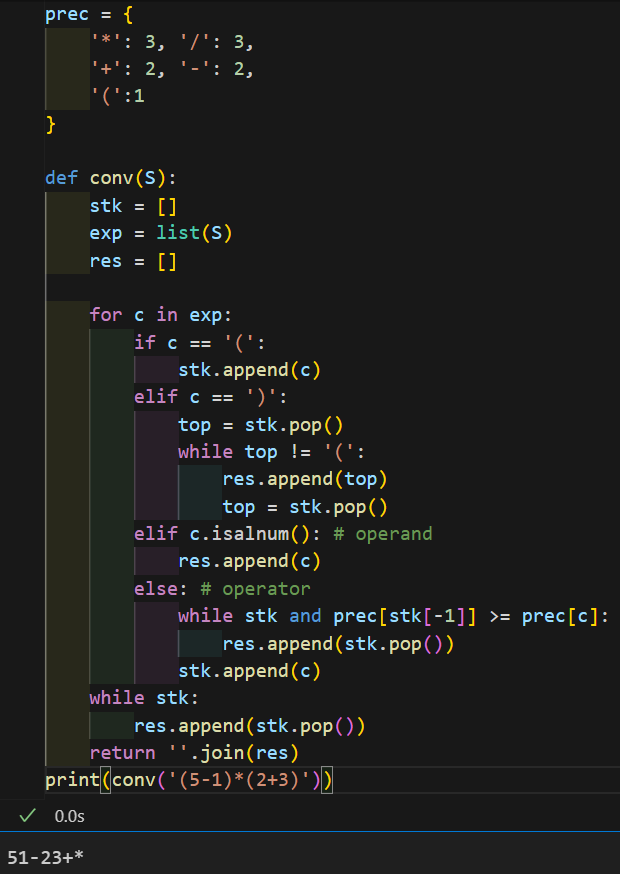
따로 추상 자료형 없이 그냥 리스트로 함

Postfix in Action
더보기
class ArrayStack:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def push(self, item):
self.data.append(item)
def pop(self):
return self.data.pop()
def peek(self):
return self.data[-1]
def splitTokens(exprStr):
tokens = []
val = 0
valProcessing = False
for c in exprStr:
if c == ' ':
continue
if c in '0123456789':
val = val * 10 + int(c)
valProcessing = True
else:
if valProcessing:
tokens.append(val)
val = 0
valProcessing = False
tokens.append(c)
if valProcessing:
tokens.append(val)
return tokens
def infixToPostfix(tokenList):
prec = {
'*': 3,
'/': 3,
'+': 2,
'-': 2,
'(': 1,
}
opStack = ArrayStack()
postfixList = []
for token in tokenList:
if isinstance(token, int):
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while(not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return postfixList
def postfixEval(tokenList):
operandStack = ArrayStack()
for token in tokenList:
if isinstance(token, int):
operandStack.push(token)
else:
operand2 = operandStack.pop()
operand1 = operandStack.pop()
if token == '+':
result = operand1 + operand2
elif token == '-':
result = operand1 - operand2
elif token == '*':
result = operand1 * operand2
elif token == '/':
result = operand1 / operand2
operandStack.push(result)
return operandStack.pop()
def solution(expr):
tokens = splitTokens(expr)
postfix = infixToPostfix(tokens)
val = postfixEval(postfix)
return valBinary Search Tree
더보기
insert, remove 특히 remove 부분 복잡함
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
def insert(self, key, data):
if self.key > key:
# go left
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key, data)
elif self.key < key:
# go right
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else: # dupe
raise KeyError("You shall not dupe.")
def lookup(self, key, parent=None):
if key < self.key:
if self.left:
return self.left.lookup(key, self)
else:
return None, None
elif key > self.key:
if self.right:
return self.right.lookup(key, self)
else:
return None, None
else:
return self, parent
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
def countChildren(self):
count = 0
if self.left:
count += 1
if self.right:
count += 1
return count
class BinSearchTree:
def __init__(self):
self.root = None
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else:
self.root = Node(key, data)
def lookup(self, key):
if self.root:
return self.root.lookup(key)
else:
return None, None
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
# damn comments
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
# The simplest case of no children
if nChildren == 0:
if parent:
if parent.key > node.key: # left
parent.left = None
else:
parent.right = None
else:
self.root = None # essentially deleting itself
# When the node has only one child
elif nChildren == 1:
if node.left:
jurassic_park = node.left
else:
jurassic_park = node.right
if parent:
if parent.key > node.key:
parent.left = jurassic_park
else:
parent.right = jurassic_park
else:
self.root = jurassic_park
# When the node has both left and right children
else:
parent = node
successor = node.right
while successor.left:
parent = successor
successor = successor.left
node.key = successor.key
node.data = successor.data
if successor.key < parent.key:
if successor.right:
parent.left = successor.right
else:
parent.left = None
else: # moot?
if successor.right:
parent.right = successor.right
else:
parent.right = None
return True
else:
return False
Data Structure
Linked List (1 based index)
더보기
뒤쪽으로만 링크가 있음.
헤드에 Dummy를 붙여서 인덱싱이 용이하게 해둠
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = None
self.head.next = self.tail
def traverse(self):
result = []
curr = self.head
while curr.next:
curr = curr.next
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
newNode.next = prev.next
if prev.next is None:
self.tail = newNode
prev.next = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos != 1 and pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
if prev.next is None:
return None
curr = prev.next
if curr.next is None:
self.tail = prev
prev.next = curr.next
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount: raise IndexError
if pos == 1:
return self.popAfter(self.head)
prev = self.getAt(pos - 1)
return self.popAfter(prev)Doubly Linked List
더보기
양방향 링크, 양방향 Dummy.
빠르지만 오버헤드가 클 듯 하다.
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def concat(self, L):
true_tail_self = self.tail.prev
true_head_target = L.head.next
true_tail_self.next = true_head_target
true_head_target.prev = true_tail_self
self.tail = L.tail
self.nodeCount += L.nodeCount
return True
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
target = prev.next
next = target.next
prev.next = next
next.prev = prev
self.nodeCount -= 1
return target.data
def popBefore(self, next):
target = next.prev
prev = target.prev
next.prev = prev
prev.next = next
self.nodeCount -= 1
return target.data
def popAt(self, pos): # raise
if pos < 1 or pos > self.nodeCount:
raise IndexError("You're better than that?!")
prev_neighbor = self.getAt(pos - 1)
return self.popAfter(prev_neighbor)BFS with Queue
더보기
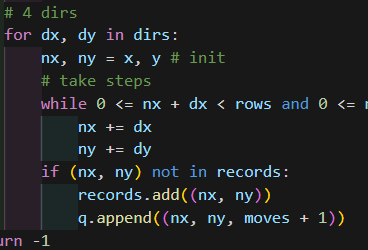
한방향으로 쭉 가는걸 루프 없이 수학적으로 구현 못하나😗
Ricochet robot 문제: 큐를 순회해서 bfs 해결

Circular Queue
더보기
지렁이큐
class CircularQueue:
def __init__(self, n):
self.maxCount = n
self.data = [None] * n
self.count = 0
self.front = -1
self.rear = -1
def size(self):
return self.count
def isEmpty(self):
return self.count == 0
def isFull(self):
return self.count == self.maxCount
def enqueue(self, x):
if self.isFull():
raise IndexError('Queue full')
self.rear = (self.rear + 1) % self.maxCount
self.data[self.rear] = x
self.count += 1
def dequeue(self):
if self.isEmpty():
raise IndexError('Queue Empty')
self.front = (self.front + 1) % self.maxCount
x = self.data[self.front]
self.count -= 1
return x
def peek(self):
if self.isEmpty():
raise IndexError('Queue Empty')
return self.data[(self.front + 1) % self.maxCount]Priority Queue
더보기
힙이랑 이거 매우중요 ...
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr.next.next:
curr = curr.next
s += repr(curr.data)
if curr.next.next is not None:
s += ' -> '
return s
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def reverse(self):
result = []
curr = self.tail
while curr.prev.prev:
curr = curr.prev
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
curr = prev.next
next = curr.next
prev.next = next
next.prev = prev
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
prev = self.getAt(pos - 1)
return self.popAfter(prev)
def concat(self, L):
self.tail.prev.next = L.head.next
L.head.next.prev = self.tail.prev
self.tail = L.tail
self.nodeCount += L.nodeCount
class PriorityQueue:
def __init__(self):
self.queue = DoublyLinkedList()
def size(self):
return self.queue.getLength()
def isEmpty(self):
return self.size() == 0
def enqueue(self, x):
newNode = Node(x)
curr = self.queue.head
while curr.next.data is not None and x <= curr.next.data:
curr = curr.next
self.queue.insertAfter(curr, newNode)
def dequeue(self):
return self.queue.popAt(self.queue.getLength())
def peek(self):
return self.queue.getAt(self.queue.getLength()).dataBinary Tree
더보기
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l + r + 1
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return l + 1 if l >= r else r + 1
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return traversal
def postorder(self):
trav = []
if self.left:
trav += self.left.postorder()
if self.right:
trav += self.right.postorder()
trav.append(self.data)
return trav
class ArrayQueue: # (temporary) for the BFS method
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
class BinaryTree:
def __init__(self, r):
self.root = r
def size(self):
if self.root:
return self.root.size()
else:
return 0
def depth(self):
if self.root:
return self.root.depth()
else:
return 0
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def postorder(self):
if self.root:
return self.root.postorder()
else:
return []
def bft(self): # the breadth first search
q = ArrayQueue()
if self.root: q.enqueue(self.root)
res = []
while not q.isEmpty():
r = q.dequeue()
res.append(r.data)
if r.left:
q.enqueue(r.left)
if r.right:
q.enqueue(r.right)
return resHeap, 1 based index
더보기
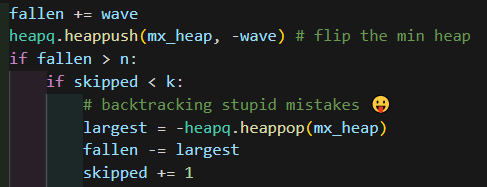
힙을 사용해서 백트래킹 해봄
완전 트리(1차원으로 표현했을 때 왼쪽부터 전부 채워져있는, 즉, 오른쪽 노드만 있는 노드는 없는 트리)
인덱스의 두배는 자식(왼쪽), 나누기 2는 부모
아래는 힙을 이용한 방어게임 솔루션 snippet

기타 미세 팁
- for - else 문: for 문이 break없이 전부 루프 했을 때 실행 됨
- dict().get(key, default) + increment: value가 부재일 때 default 넣어줘서 편함 -> goodbye if not dict().get() !!!
- enumerate(iter, start=i): enumerate 함과 동시에 시작 인덱스 지정 가능 -> 그것도 몰랏다니...
기타 문제들
- 프로그래머스 코드 테스트 부분 참조
- DP 다른 문제 찾아서 풀어볼 것